Do Data Policy Restrictions Impact the Productivity Performance of Firms and Industries?
Published By: Martina F. Ferracane Erik van der Marel Guest Author
Research Areas: Digital Economy DTE Services
Summary
This paper examines how policies regulating the cross-border movement and domestic use of electronic data on the internet impact the productivity of firms in sectors relying on electronic data. In doing so, we collect regulatory information on a group of developed economies and create an index that measures the regulatory restrictiveness of each country’s data policies. The index is based on observable policy measures that explicitly inhibit the cross-border movement and domestic use of data. Using cross-country firm-level and industry-level data, we analyse econometrically the extent to which these data regulations over time impact the productivity performance of downstream firms and industries respectively. We show that stricter data policies have a negative and significant impact on the performance of downstream firms in sectors reliant on electronic data. This adverse effect is stronger for countries with strong technology networks, for servicified firms, and holds for several robustness checks.
Corresponding author: [email protected], Senior Economist at ECIPE & Université Libre de Bruxelles (ULB) and ECARES, Avenue des Arts 40, 1000, Brussels; Martina Francesca Ferracane, [email protected], PhD candidate at Hamburg University, Policy Leader Fellow at the European University Institute (EUI) and Research Associate at ECIPE; Janez Kren, [email protected], PhD candidate at the University of Leuven. We thank Giorgio Garbasso, Nicolas Botton, Valentin Moreau, Cristina Rujan for their excellent research assistance. We would also like to thank Stela Rubinova, Julian Nyarko, Sébastien Miroudot, Ben Shepherd and Hosuk Lee-Makiyama as well as participants of the 5th PEPA/SIEL Conference at Tilburg University, the 34th Annual Conference of the European Association of Law and Economics (EALE), the PEP Digital Information Policy Scholars Conference at George Mason University, and the Services-Led Development Conference at the ADBI in Tokyo for their useful comments on earlier drafts.
1. Introduction
Between 2000 and 2015, global traffic of data over the internet rose by a factor of 863. This represented an annual compound growth rate of 62.1 percent (Figure 1). For many firms the amplified use of data has become an essential element of the production processes in the current digital era, aiming to increase their economic performance. At the same time, many governments have started to regulate the use and transfer of data over the internet. These policies are likely to have an impact on the productivity performance of firms.
This paper investigates whether measures regulating electronic data have an impact on firms’ productivity. We do so by employing a cross-country analysis over time of policy measures on the use and transfer of data for a group of developed economies. To our understanding, this paper makes a unique contribution to the literature by showing how regulatory policies on data have an impact on the firm’s productivity performance. In particular, we assess how stricter data policies affect the firm’s productivity in downstream sectors relying on data. Our policy frameworks on data across countries cover both how the flow of data across borders and the domestic use of data are regulated.
We define data policies as those regulatory measures that restrict the commercial use of electronic data. We limit our analysis to policy measures which are implemented at the national or supranational level (such as the EU). Although there is a great number of data policies implemented by local public entities, these are not the policies on which we focus on this paper. We identify two main categories of data policies. The first category covers those policies that impact the cross-border transfer of data; the second category covers policies that apply to the use of data domestically. The former category deals with all measures that raise the cost of conducting business across borders by either mandating companies to keep data within a certain border or by imposing additional requirements for data to be transferred abroad. The latter category refers to all measures that impose certain requirements for firms to access, store, process or more generally make any commercial use of data within a certain jurisdiction.
Investigating the relationship between the regulatory approaches countries apply on the domestic use and cross-border transfer of data and the performance of downstream firms requires three novel datasets that we have uniquely developed. These are (a) information on how restrictive countries are regarding the domestic use and cross-border transfer of electronic data, (b) a measure of cross-country performance of firms and finally (c) an indicator measuring the extent to which sectors use data as part of their production process.
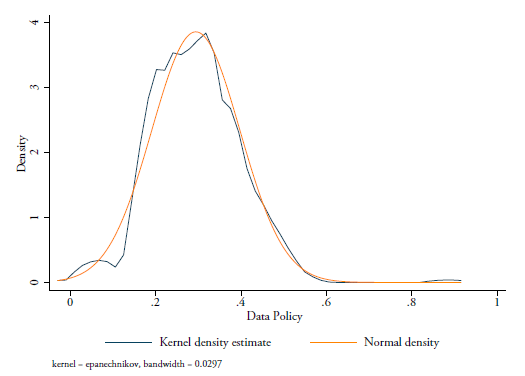
Regarding the first set of information, we have created a quantifiable and detailed set of policy information on the regulatory framework of 64 economies towards the use and cross-border transfer of data as developed in Ferracane et al. (2018). This comprehensive dataset contains extensive information on the state and history of data policies. This information on data policies has been condensed into a composite (weighted) time-varying policy index for each country covered. The data policy index takes on values ranging between 0 (completely open) to 1 (virtually closed) with intermediate scores reflecting varying degrees of applied policy restrictions on the use and cross-border transfer of data. The creation of this database together with its corresponding index represents in itself a major contribution to the existing literature, which can be used for future research in this area.
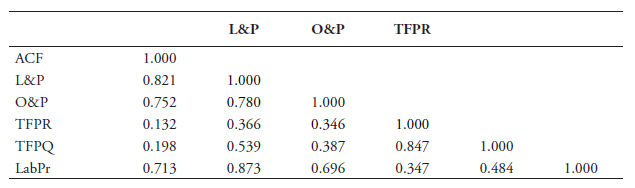
For our second set of information on the performance of firms, we use consistent firm-level data over a group of developed economies from the ORBIS database. In particular, we exploit the TFP estimate recently developed by Ackerberg et al. (2015) which has been applied in various studies such as Arnold et al. (2015) and Fernades and Paunov (2012). The productivity literature has put forward several empirical methodologies for constructing a credible TFP indicator with estimation strategies from Olley and Pakes (1996) and Levinsohn and Petrin (2003) as the most commonly used ones. The TFP measure by Ackerberg et al. (2015) improves on the previous two approaches by addressing their collinearity problem. In this paper, we use this Ackerberg TFP estimate throughout all our regressions, but also perform robustness checks with the alternative TFP proxies to compare the results, including Hsieh and Klenow’s (2014; 2009) TFPR and TFPQ measures.
Finally, our third set of information is an indicator measuring the extent to which different sectors use data as part of their production process. This indicator links up the cross-country TFP estimates of firms and the index on countries’ data policies with input shares that measure the reliance on data for each sector. This identification strategy weights each country’s state of data policies with each sectors’ dependence on data as an input. The use of data for each sector is computed in an exogenous manner by taking detailed input-output coefficients from a country not part of our analysis, namely the US. Employing this methodology assumes that sectors which employ comparatively more data in their production process are more affected by the changes in data policies.
We perform our analysis in a cross-country panel setting. The results show that stricter more restrictive data policies do indeed have a significant negative impact on the productivity performance of firms in downstream data-intense sectors. In addition, we find that this negative impact is stronger for countries with a better digital-enabling environment and for manufacturing firms that also produce services. Moreover, the results are robust when correcting for other regulatory policies in services sectors following Arnold et al. (2015; 2011). In the analysis, we apply the appropriate fixed effects and control variables, and take account of the potential reverse causality by applying a lag between the time of implementation of the data policies and the measurement of firms’ productivity. In addition, we also split out our main index of data policies into different types of policies, namely policies that affect the domestic use of data and the ones that affect the cross-border movement of data to see whether the two individual sub-indexes have a different impact on firm productivity.
Our work contributes to the existing literature in three ways. First, to our knowledge, we are the first to create a dataset in which the regulatory framework of countries regarding data has been quantified from a descriptive into a measurable index. Although existing works have undertaken a similar exercise with respect to other regulatory policies on services (Arnold et al., 2015) or more generally on non-tariff barriers (Kee et al., 2009), to date no work has made a similar effort for data policies. Second, we relate our policy index to micro-level data on the productivity performance of firms across a group of countries. This departs from much of the previous research that is based on a single country and allows us to exploit cross-country differences as an additional source of variation. It also allows us to use industry-year fixed effects to control for possible changes. Furthermore, having a group of countries makes it possible to extrapolate policy conclusions across countries. Third, we provide robust evidence on the way in which these data-related policies affect the productivity of firms that are more dependent on data.
The rest of this paper is organised as follows. The next section discusses the previous literature regarding the use and cross-border transfer of data and their related economic effects. Section 3 elaborates on the three sets of data used in this paper. It also provides some descriptive analysis on how the use of data in different sectors relates to productivity. Section 4 presents the estimation strategy and Section 5 reviews the estimation results. Finally, the last section concludes by putting the results in a wider context.
2. Related Literature
This paper closely relates to the previous literature on the effect of restrictive services policies on downstream firm productivity such as Arnold et al. (2015; 2011). In line with their work on services, the identification strategy in this paper weighs an index on restrictive data policies by the share of input use of data for each downstream sector. This value is then regressed on firm-level TFP.[1] The reason for using a similar methodology is that policy restrictions on data relate closely to services regulation as many digital services depend on the use and transfer of data for their business. For instance, Opresnik and Taisch (2015) show that data is generated through the use of services in the production processes of firms and that this data is exploited in later stages of the production process for more innovative activities and new services for consumers. This allows for an increased value extraction using big data and, as a result, data-related services become increasingly an essential factor to improve the firms’ productivity.[2]
This paper takes a similar line. More restrictive data policies are expected to have an adverse effect on downstream firms in sectors that depend on data in their production process. Today many firms in data-intense sectors rely heavily on data and therefore policies that restrict the use and cross-border transfer of data are expected to reduce their efficiency and eventually productivity. Yet, data policies have only come under the spotlight in recent years as a consequence of the widespread adoption of cloud computing services and the increased cross-border provision of services over the internet.
The empirical research on data policies and firms’ productivity is relatively scarce. To the best of our knowledge, van der Marel et al. (2016) is the only study that explores how regulatory policies related to electronic data affect TFP, albeit at an industry-level. The authors make a first attempt at analysing this linkage econometrically by setting up a data regulatory index using existing indices of services regulation. They calculate the costs of data policies for domestic firms by establishing a link between regulation in data services and TFP at the industry-level in downstream sectors across a small set of countries. They find that stricter data policies tend to have a stronger negative impact on the downstream performance of industries that are more data-intense. They also employ their econometric results in a general equilibrium analysis using the Global Trade Analysis Project (GTAP) to estimate the wider macroeconomic impact.
Other studies have looked specifically at one policy framework regarding data, namely the EU General Data Protection Regulation (GDPR). Christensen et al. (2013) uses calibration techniques to evaluate the impact of the GDPR proposal on small- and medium-sized enterprises (SMEs) and concludes that SMEs that use data rather intensively are likely to incur substantial costs in complying with these new rules. The authors compute this result using a simulated dynamic stochastic general equilibrium model and show that up to 100,000 jobs could disappear in the short-run and more than 300,000 in the long-run. Another study by Bauer et al. (2013) uses a computable general equilibrium GTAP model to estimate the economic impact of the GDPR and finds that this law could lead to losses up to 1.3 percent of the EU’s GDP as a result of a reduction of trade between the EU and the rest of the world.
Our study builds on these aforementioned works by bringing new contributions. First of all, we contribute to the general literature on services regulation by focusing on one particular policy area, namely restrictions related to the domestic use and cross-border movement of data. Currently, many data flow disciplines are being discussed as part of various negotiations at the World Trade Organization (WTO) and regional trade agreements. Yet, to date no thorough empirical study has undertaken an effort to find a significant effect of these measures on productivity and trade. Second, we construct a regulatory index measuring the restrictiveness of data policies. The data policy index considers a set of policies that impose a substantial cost on the use and cross-border movement of data and are therefore expected to increase the costs for the provision of downstream goods and services. In turn, this would have an impact on the productivity of the firm, which we measure with firm-level data.
Building on this approach, this paper follows Iootty et al. (2016) which uses cross-country productivity data of firms covering a wide set of developed economies using ORBIS to come up with several firm-level TFP measures of productivity. Gal and Hijzen (2016), among others, also use cross-country firm-level data of productivity sourced from the same ORBIS database to measure the economic performance of firms. However, in their paper, the authors use a broader measure of output performance whereas we specifically employ TFP. Moreover, both Iootty et al. (2016) and Gal and Hijzen (2016) analyse the productivity impact of a wider set of policy measures of overall product market reform or in services and not of data policies in particular.
In short, our study combines all aforementioned works by using an identification strategy similar to Arnold et al. (2015; 2011) but applied to data policies, for a wider set of countries and by developing specific cross-country TFP performance at the firm level.
[1] Other previous works that employ similar identification strategy with firm-level productivity data in a services context are Fernades and Paunov (2012) and Duggan et al. (2013) with each using a different TFP proxy.
[2] Recent work by Goldfarb and Trefler (2018) discus the potential theoretical implications of data policies such as data localisation and privacy regulations on trade although this is put in a broader context of Artificial Intelligence (AI). Nonetheless, the authors do make clear that an expanded AI industry in which data flows are an important factor would have clear implications for trade in services. Similarly, Goldfarb and Tucker (2012) point out that privacy regulations may harm innovative activities by presenting the results of previous studies undertaken with respect to two services sectors, namely in health services and online advertising. Both studies show that there are strong linkages between the effective sourcing and use of data, services sectors and services trade.
3. The Data
To perform our empirical analysis, we need three sets of data: a regulatory index for the use and cross-border transfer of data; a measure of TFP performance at the firm level; and input-output coefficients measuring the extent to which downstream (manufacturing and services) sectors use data as inputs. These input-output coefficients are then interacted with the data policy index to have a weighted score of regulatory restrictiveness.
3.1 Data Policy Index
The first essential ingredient for our analysis is a quantifiable and detailed set of policy information on countries’ regulatory framework on data. We draw on a comprehensive new database of data policies recently released by the European Centre for International Political Economy (ECIPE) to estimate our data policy index.[1] The policies used for the analysis are those considered to create a cost for firms relying on data for their businesses. The criteria for listing a certain policy measure in the database are the following: (i) it creates a more restrictive regime for online versus offline users of data; (ii) it implies a different treatment between domestic and foreign users of data; and (iii) it is applied in a manner considered disproportionately burdensome to achieve a certain policy objective.
Starting from the database, these policies are aggregated into an index using a detailed weighting scheme adapted from Ferracane et al. (2018) and presented in detail in Annex A.[2] We expand the index released by Ferracane et al. (2018), which covered only the years 2016/2017, to create a panel for the years 2006-2017 that we can use in our regressions. In addition, the database and the index have been updated with new regulatory measures found in certain countries.
To build up the index, each policy measure identified in any of the categories receives a score that varies between 0 (completely open) and 1 (virtually closed) according to how vast its scope is. A higher score represents a higher level of restrictiveness in data policies. While certain data policies can be legitimate and necessary to protect non-economic objectives such as the privacy of the individual or to ensure national security, these policies nevertheless create substantial costs for businesses and are therefore listed in the database.
After applying our weighting scheme, the data policy index also varies between 0 (completely open) and 1 (virtually closed). The higher the index, the stricter the data policies implemented in the countries. Moreover, the index is broken down into two sub-indexes that cover two main types of policy measures that we analyse in this paper: one sub-index that covers policies on the cross-border movement of data and one sub-index covers policies on the domestic use of data. Analysing these two sub-indexes separately provides additional information on whether the impact of data policies on firms’ productivity varies according to the nature of the policies. The full data policy index is measured as the sum of these two sub-indexes. The list of measures included in the two sub-indexes is summarised in Table 1 and the specific weight for each measure is given in the last column. Table 2 shows the values of the data policy index and the two sub-indexes for the year 2017.
As shown in Table 1, the sub-indexes are measures as a weighted average of different types of measures. The weights are intended to reflect the level of restrictiveness of the types of measures in terms of costs for the firm. The first sub-index on cross-border data flows covers three types of measures, namely (i) a ban to transfer data or a local processing requirement for data; (ii) a local storage requirement, and (iii) a conditional flow regime. The second sub-index covers a series of subcategories of policies affecting the domestic use of data. These are: (i) data retention requirements, (ii) subject rights on data privacy, (iii) administrative requirements on data privacy, (iv) sanctions for non-compliance, and finally, (v) other restrictive practices related to data policies.
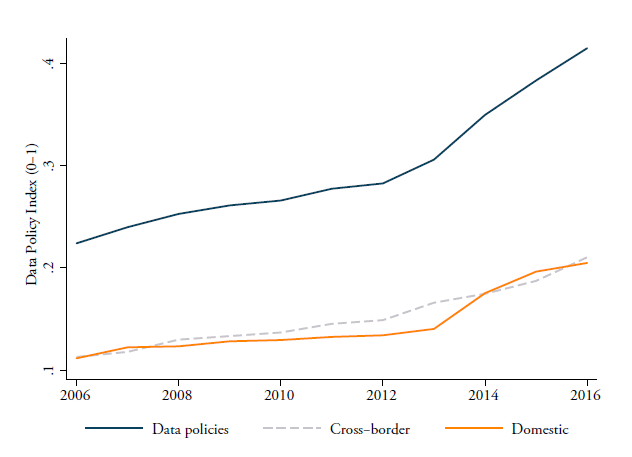
Figure 2 shows how the two sub-indexes and the overall data policy index have evolved over time between the years 2006 and 2016. Each line is a (weighted) average of the 64 countries covered in this study. As one can see, there is a clear upward trend reflecting the fact that all types of data policies are becoming stricter over time. Note that measures affecting the cross-border data flows can directly inhibit the free flow of data across countries and therefore can directly restrict trade in services. On the other hand, measures belonging to the second sub-index on the domestic use of data only indirectly affect the flow of data across borders and therefore are expected to create costs for trade only indirectly.
3.2 Firm-level Performance
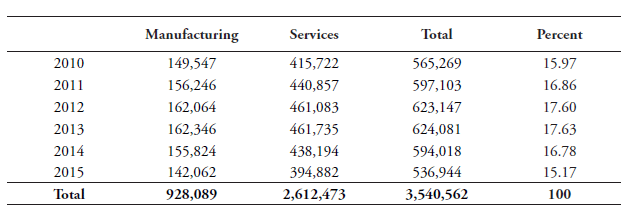
The firm-level data for estimating our TFP measures is retrieved from the ORBIS database from Bureau van Dijk (BvD). Although our aim is to include as many developed countries as possible that are covered by our index, unfortunately, ORBIS does not report all variables needed to calculate TFP for all 64 countries. Moreover, some smaller states such as Luxembourg, Malta and Cyprus have only few observations. Therefore, we limit the analysis to EU countries, Japan and Korea.[3] Data in ORBIS is substantially improved from 2005 onwards. As said before, both manufacturing and services firms are considered in our computations to take stock of the wider downstream economy. Most services sectors are relatively more dependent on data in terms of creating value-added than manufacturing industries, which is the main reason why they are included. See Table B1 in Annex B for a yearly overview of firm observations for services and goods.
One word of caution is warranted for our firm-level observations. Although we would prefer to have an entirely balanced panel dataset with only surviving firms, in our case this wish appears to be difficult. Our preferred time frame is 2006-2015 which covers a less than perfect panel format of surviving firms. Moreover, ORBIS provides a poor track of firms that enter and exit. In case we were to use only surviving firms with a shorter time frame after 2010, our observations would drop by 60 percent. In large part, this is due to the few firms that are actually consistently present in ORBIS. Therefore, we prefer to work with data starting in 2006. Moreover, the policy trends across our sample of countries become visible after 2006, which provides a good opportunity to exploit the variation in policy changes, albeit with the trade-off of an unbalanced panel dataset.
Firm-level TFP measures can be computed in different ways. Over the years, various methodologies have been developed in the literature that have been taken up in recent empirical works. TFP measures by Olley and Pakes (2003) (O&P) and Levinsohn and Petrin (2008) (L&P) are the most commonly used. More recently, several papers that are close to our line of research such as Fernandes and Paunov (2012) and Arnold et al. (2015) have instead used the TFP estimation developed by Ackerberg et al. (2015) (ACF). Although all three approaches correct for the endogeneity of input choices, including the choice of services as inputs, Ackerberg et al. (2015) improves the former two methods by correcting for potential collinearity problems. This problem could otherwise occur from a distorting factor with regards to the identification of the variable input coefficients. Ackerberg et al. (2015) also provide correction for the timing of input choice decision.
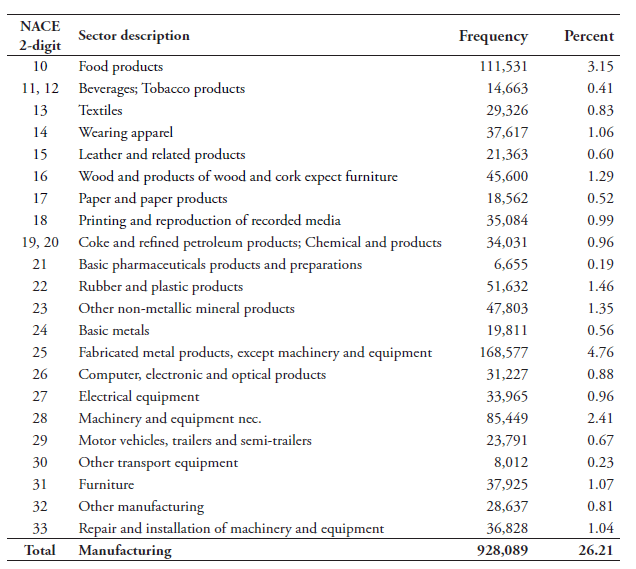
This estimation approach is also preferred in our paper and we use it in all our regressions. To obtain TFP, one needs to estimate production functions. Since we are dealing with multiple countries and multiple industries, we estimate these production functions for each 2-digit NACE Rev. 2 sector and by country. This allows for industries and countries to differ in their production technology. In some cases, we regroup countries and industries due to their insufficient number of observations.[4] In total there are 52 industry groupings that can be seen in Table B2 and B3 in Annex B together with an overview of firm observations.[5] Table B4 reports the number of firm observations by the 18 country groupings.
To start estimating the production functions we need firm-level data on value-added. Normally, firm-level value-added is defined as sales minus the value of intermediate inputs, which includes materials, services and energy. In ORBIS, unfortunately, only operating net revenue and material costs are reported and therefore we are bound to use these two variables to compute value-added.
Moreover, materials are not reported for any firm for some European countries.[6] For these countries, we use proxy material inputs. The way we do so is based on Basu et al. (2009) in which the authors compute materials as operational revenue minus operational profits, wages and depreciation. Since this is a less precise measure of material inputs, we check whether a strong correlation exists between both measures: the direct and proxied approach for all countries that report the two methods. Table B5 reports the regressions as correlations of the indirect measure on materials reported directly for these countries. The result shows that correlations are very strong with a high R-squared. Once we use this method of proxy, the number of firms in our dataset increases by 11 percent.[7]
The production functions themselves are estimated using the standard approach of Cobb-Douglas in logarithmic form, as shown in the following equation:
In equation (1), Yit stands for value-added output of a firm i in year t and represents the variable of value-added as explained above with the caveats described. Kit denotes the capital stock of a firm and is calculated based on the Perpetual Inventory Method (PIM) using real fixed tangible assets, whilst Lit designates the labour input of a firm, which is proxied by the number of employees. Furthermore, ωit is the unobserved total factor productivity and∈it is the random iid shock. As explained in the introduction of this section, we do not use OLS to estimate equation (1) as this estimation strategy suffers from simultaneity bias in its inputs. Instead, we use the approach from Ackerberg et al. (2015). For this specification, the material inputs are used as a proxy to obtain for unobserved time-varying productivity (ωit).
Of note, we deflate all three variables from nominal into deflated values first and then put them in Euros using constant 2010 exchange rates. Data on prices for EU countries come from Eurostat’s National Accounts database, and for Japan and Korea from OECD Structural Analysis database (STAN). Our deflators are mostly available at the 2-digit NACE industries. In case price data are missing, we use either a higher level of aggregation or otherwise simple GDP deflators. For value-added, we use the value-added in gross price index (i.e. implicit deflator) in constant prices with 2010 as the reference year for all countries. For materials, we use a deflator for intermediate consumption and finally for capital stock we use the consumption of fixed capital price index.
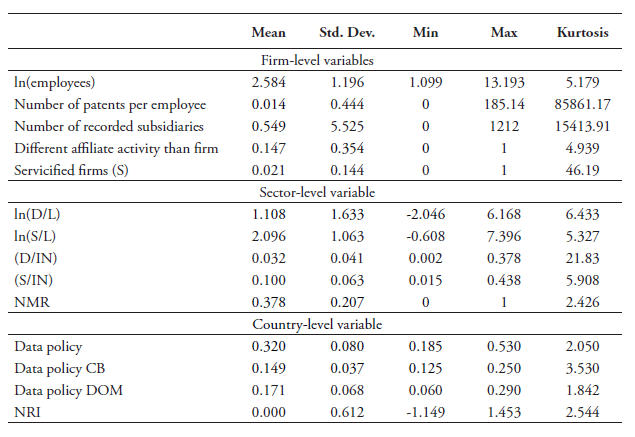
The parameters βK and βL of the production functions are estimated separately by 18 countries times 52 sectors. This provides us with a total of 936 production functions.[8] They are estimated only with firms that consistently report values for at least four years, in order to remain in line with previous works. All in all, based on the unbiased Ackerberg approach sets of estimates, we obtain a firm-level, country-specific, time-varying logarithmic TFP estimates. In Annex B, Table B7 provides summary statistics for the variables used in equation (1) production function whilst Tables B8 and B9 show summary statistics for all our TFP estimates.
3.3 Input-Output Coefficients of Data
The extent to which different sectors are using data as an input is measured through US input-output Use tables from the Bureau of Economic Analysis (BEA). These input-output matrices are at the 6-digit NAICS level, which allows us to identify at a disaggregated level those sectors that are more reliant on data as part of our identification strategy. Another motivation for using US tables is that the US is not included as part of our firm-level data. This makes our input coefficients on data use exogenous. There is a debate in the economic literature about whether one should use the assumption of equal industry technologies across countries or not. Equal technology coefficients seem reasonable if one thinks that the countries selected in the sample are reasonably similar in their economic structures and technology endowments.[9] This is likely to be true in our case as we are dealing with developed economies only.
In computing these data input coefficients, or data-intensities, we must first determine the sectors that provide data services to other downstream sectors. Table 3 lists these sectors which we call “data producers”. They are sectors that deploy a high intensity of electronic data when providing services. As such, these sectors act as an input of data to other sectors of the economy. This selection of sectors follows van der Marel et al. (2016) and is in line with Jorgenson et al. (2011) regarding IT-producing and using industries.[10] The selected sectors include, inter alia, telecommunication; data processing, hosting and related services; internet service providers and web search portals; software publishers; computer system design services and other computer-related services.
We calculate data services intensities for each downstream manufacturing and services sector at the 6-digit level in two ways. The first is the ratio of the value of data services inputs over labour of each downstream sector, while the second consists in the share of data services inputs that each sector uses as part of its total input based on purchaser’s prices. These latter input shares are referred to in the economic literature as backward linkages.[11] The inputs share over labour ratios are more in line with factor intensities put forward in the comparative advantage literature (e.g. Chor, 2011; Nunn, 2011). Labour is sourced from the US Bureau of Labour Statistics in NAICS for the same year and is matched with the US BEA input-output matrix which fits neatly. Our preferred proxy for intensities is the ratio of data input use over labour which is used in our baseline regression, but the inputs shares are also used as part of our robustness checks.
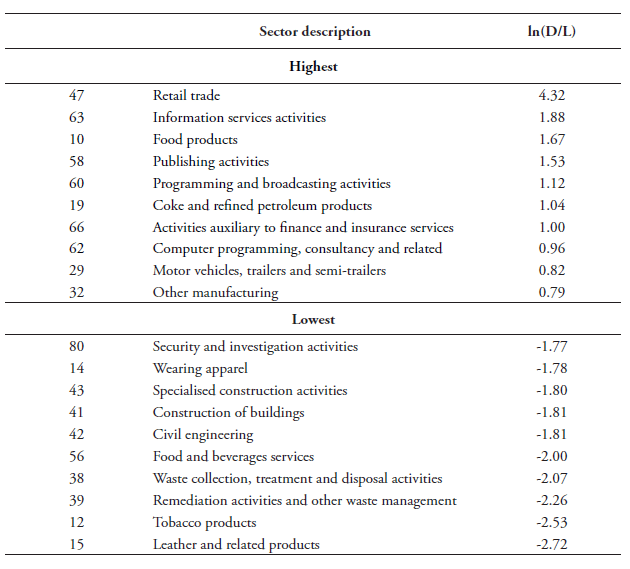
Table 4 provides an overview of the Top 10 sector with the highest and lowest ratios of data-intensities over labour by 2-digit NACE Rev.2, whereas Table 5 presents a similar Top 10 list of the data-intense services based on input shares. The reason for re-classifying these input-coefficients is that our firm-level data is provided in NACE. Since no concordance table currently exists between the original 6-digit BEA IO code table to the 6-digit NAICS and then to the 4-digit NACE, we have developed our own table and aggregated these data input coefficients at the 2-digit level for both types of intensities.[12] Note that for some 4-digit NACE sectors, input coefficients are still missing after concording. To complete the reclassification, we take the average of all other 4-digit NACE sectors that belong to the same 2-digit sector. In the few cases where input data is not available at the 4-digit level, we take data from one or two levels higher up in the classification table, namely for the 3 or 2-digit NACE sectors, and compute the average.[13]
As shown in Tables 4 and 5, sectors relying the most on data as inputs, which we define as “data users”, include unsurprisingly sectors such as telecommunications, information services and computer programming services. These data producing sectors are also the highest data using sectors. However, somewhat less obvious sectors are also listed as intense data users such as retail trade or real estate services. Other sectors that are found to be data-intense are head office services and management consultancy services, programming and broadcasting, and professional, scientific and technical services. We also find financial and insurance services are data-intense sectors, which is in line with the fact that these sectors are also technology-intensive. On the other side of the spectrum, we find sectors such as construction, tobacco products, wearing apparel, coke and petroleum, beverage and food products rely the least on data as inputs.
3.4 Descriptive Analysis
Using these two types of data-intensities, we come up with some preliminary analytical intuitions on the direction of the relationship between data-intensities and productivity. Figure 2 plots these two variables in which, on the horizontal axis, our preferred TFP measure is averaged over each 2-digit NACE sector (across all countries) whilst the vertical axis gives the ratio of data use over labour. In this figure, a positive association between the two variables appears, which indicates that sectors which are more data-intense, and therefore more reliant on data-use in their production, are also the ones that show higher TFP rates. Note that retail services and tobacco products are excluded from this sample (but not in the regressions) because they are extreme outliers. On the whole, however, one can see that various services are very productive whilst also having a high share of data inputs. Other sectors such as beverages or the rubber and plastics industry show low TFP rates and also have lower shares of data-inputs.
Figure 3 replicates Figure 2 but now exclusively focuses on services sectors. This figure again shows a positive association between TFP and data-intensities. Services such as telecommunications, publishing activities, but also employment services or head office and consultancy services, are assessed as most data-intense whilst also displaying a higher level of TFP. On the one hand, the fact that these services are the most productive is not entirely surprising as they are services that represent the most dynamic segment the services economy over the last decade. On the other hand, some traditional services such as land or freight rail transport or postal services are shown to be the least productive in terms of TFP and also exhibit a low share of data-intensity. Note that the low productivity of these services sectors could also reflect their regulatory setting which is still relatively restrictive in many countries in our sample.
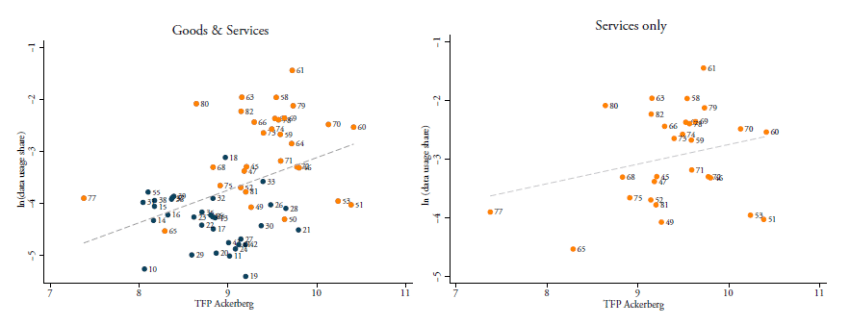
Similar scatter plots are developed in Figure 4 but now using the share of data use in total input use. The left-hand panel in this figure shows the correlation between this intensity and TFP when taking goods and services together, whilst the right-hand panel shows this relationship for services only. Again, in both panels there is a positive relationship, suggesting that more data-intense sectors generally have higher productivity levels. This result somehow stands in contrast with the general notion that services suffer from ailing productivity in most developed economies and that they are less productive compared to manufacturing. To perform a robustness check, Figure 5 repeats the previous scatter plots using both types of data-intensities but this time using labour productivity (i.e. value-added over labour). A weaker association between data input over labour appears in the left-hand panel, while the relationship becomes negative when using data shares in the right-hand panel. The latter panel suggests that goods industries show higher labour productivity than many services sectors whilst being less data-intense.
[1] The authors have contributed to the development of the database at ECIPE. The dataset comprises 64 economies and is publicly available on the website of the ECIPE at the link: www.ecipe.org/dte/database. Besides analysing the 28 EU member states and the EU economy as a single entity, this database also covers Argentina, Australia, Brunei, Canada, Chile, China, Colombia, Costa Rica, Ecuador, Hong Kong, Iceland, India, Indonesia, Israel, Japan, Korea, Malaysia, Mexico, New Zealand, Nigeria, Norway, Pakistan, Panama, Paraguay, Peru, Philippines, Russia, Singapore, South Africa, Switzerland, Taiwan, Thailand, Turkey, United States and Vietnam.
[2] The authors have previously used this categorisation in Ferracane et al. (2018a).
[3] The non-EU countries allow us to compare the impact of data regulations in developed economies outside the EU. This is particularly relevant given that the EU member states have, to some extent, a similar set of data policies.
[4] The country groupings are the following: Germany with Austria, the Benelux, Sweden with Denmark, Estonia with Latvia, and finally the UK with Ireland. The reason for choosing these groupings is each pair is fairly like-minded in their economic structures. Regarding sector division, in total we have 57 different sectors, which is considerably more than in previous studies. This is because the high number of firm observations in each sector allows us to go ahead with this selection, although some industries are also regrouped together.
[5] An interesting minor detail is that the frequency share of firm observations between services and goods closely follows their value-added composition in GDP which in 2014 for goods was 24.3 percent whilst for services this figure was 74 percent according to the World Development Indicators.
[6] These countries are Cyprus, Denmark, Greece, Ireland, Lithuania, Malta and the UK. In addition to the European countries, we also include Korea and Japan in our analysis.
[7] Note, however, that ORBIS reports only 39 firm observations for Malta and the country is therefore not included in the final dataset. Furthermore, firms from Greece, Cyprus and Lithuania have neither reported nor proxied materials in ORBIS and are therefore also excluded from any further analysis in this paper. Table B6 provides the list of countries used in the analysis.
[8] An overview of this matrix with the number of firms in each of these cells is available upon request. Of note, the production functions were estimated twice: first using the approach of proxy materials and then, second, with reported materials. However, throughout our regressions we use the proxy materials as results do not differ between the two approaches.
[9] Practically, this might as well form a convenient assumption if a suspicion exists that input-output tables at country level are not very well measured for some economies. This could be the case for less developed countries which suffer from weak reporting capacities.
[10] Furthermore, this selection of data-producing sectors is also in line with the Internet Association’s definition of internet sectors as described in Siwek (2017).
[11] Moreover, one additional reason to look at the input-side of data and data-related services is that the recent economic literature connects the potential growth and productivity performance of countries notably to the input use of data and digital services in the wider economy. See Jorgenson et al. (2011).
[12] Note that in the actual regressions we use data-intensities at 4-digit NACE level.
[13] We also computed the median in addition to the mean and used these intensities in our empirical estimations which produced similar results. The self-constructed concordance table is available upon request.
4. Empirical Strategy
This section sets out the empirical strategy. First, we develop a so-called data linkage variable. This variable is calculated by weighting the regulatory data policy index used for our regressions with the input coefficients of data-intensities for each sector. Then, in a second step, we present our baseline specification for the regressions.
4.1 Data Linkage
The empirical estimation strategy follows the one pioneered by Arnold et al. (2011; 2015) and is used in several other papers with the purpose of creating a so-called services linkage index. In our case, we develop a data linkage index. For each country, we interact the input coefficient of data input reliance for each downstream sector with the country-specific data policy index. This is an identification strategy that relies on the assumption that sectors more reliant on data as inputs are also those which are more affected by changes in data policies. This weighted approach of data policy regulation that relies on data intensities is, in our view, a more just approach to measure the impact of data policies on TFP in contrast to an unweighted one.
For this reason, each of the three country-specific data policy indexes presented in Section 3 (i.e. the full data policy index and the two data policy sub-indexes on cross-border data flows and domestic use of data) is multiplied by the two data-intensities for country c, from the list of data producing sectors d, for each downstream manufacturing and services firm in sector j. As mentioned, one data intensity is the data use φjd as a ratio over labour called (D/L) taken in logs. The second one is the data use φjd expressed as a share of total intermediate input use called (D/IN). The formula we use for these respective intensities is:
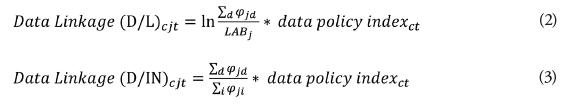 where φjd and φji come from the BEA’s input-output tables and are computed based on the value-added of inputs used. In equation (2), comes from the US Bureau of Labour Statistics (BLS) for the year 2007 and is reported at the 6-digit level NAICS but concorded into the 4-digit NACE. Then, the log is taken for this intensity. The data policy index refers to the three country-year specific regulatory indexes presented in Section 3. We choose our input-output coefficients to be industry-specific from these matrixes because Arnold et al. (2015) claim that input reliance coefficients measured at the firm level may suffer from endogeneity issues in connection with the performance of the firm.[1] This approach is well-suited since ORBIS does not report any information on data input use. Moreover, as previously explained, since we use common input-output coefficients, φcjd, from the US (rather than a country-sector specific one), our input-coefficients are even more exogenous. Of note, equation (2) and (3) are also used to assess the effect of data policies based on the two sub-indexes, that is the one on cross-border data flows and the second one on domestic regulatory policies regarding the use of data.
where φjd and φji come from the BEA’s input-output tables and are computed based on the value-added of inputs used. In equation (2), comes from the US Bureau of Labour Statistics (BLS) for the year 2007 and is reported at the 6-digit level NAICS but concorded into the 4-digit NACE. Then, the log is taken for this intensity. The data policy index refers to the three country-year specific regulatory indexes presented in Section 3. We choose our input-output coefficients to be industry-specific from these matrixes because Arnold et al. (2015) claim that input reliance coefficients measured at the firm level may suffer from endogeneity issues in connection with the performance of the firm.[1] This approach is well-suited since ORBIS does not report any information on data input use. Moreover, as previously explained, since we use common input-output coefficients, φcjd, from the US (rather than a country-sector specific one), our input-coefficients are even more exogenous. Of note, equation (2) and (3) are also used to assess the effect of data policies based on the two sub-indexes, that is the one on cross-border data flows and the second one on domestic regulatory policies regarding the use of data.
4.2 Baseline Specification
We use equation (2) in our baseline regression presented in equation (4) which measures the extent to which firm-level TFP is affected by the data linkage variable in previous years. In other words, we regress the logarithm of our Ackerberg TFP measure of manufacturing and services firms i, in country c, in industry j, in time t, on the data linkage which is applied with a lag. As in the literature, the motivation for lagging the data linkage index is due to the time it takes before downstream firms across all countries face the regulatory consequences of restrictive data policies. In addition, taking the lag further reduces endogeneity concerns to the extent that reverse causality becomes less obvious. The baseline specification takes the following form:
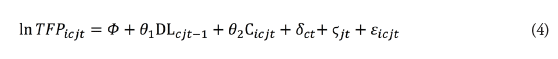 In equation (4), the terms δct and ϛjt refer to the fixed effects by country-year and sector-year respectively. Sector fixed effects are set at the 4-digit NACE level. Instead of applying firm-fixed effects, which would be too strict in our panel setting, we include several firm-level controls (Cicjt) . These control variables are taken from ORBIS and correct for the fact that larger firms usually have greater levels of productivity according to the firm-heterogeneity literature (see Bernard et al., 2003; Melitz, 2003). Therefore, we take the log of the number of employees in addition to the number of subsidiaries each firm has in order to account for the firm size. In addition, we also include the number of patents per employee each firm has obtained in order to correct for the fact that more innovative firms tend to be more productive (see Griffith et al., 2004a; 2004b).[2] We also include information on whether a firm has a foreign subsidiary or not (see below). Finally, εicjt is the residual. Regressions are estimated with standard errors which are two-way clustered by country-sector-year and firm over the years 2006-2015.
In equation (4), the terms δct and ϛjt refer to the fixed effects by country-year and sector-year respectively. Sector fixed effects are set at the 4-digit NACE level. Instead of applying firm-fixed effects, which would be too strict in our panel setting, we include several firm-level controls (Cicjt) . These control variables are taken from ORBIS and correct for the fact that larger firms usually have greater levels of productivity according to the firm-heterogeneity literature (see Bernard et al., 2003; Melitz, 2003). Therefore, we take the log of the number of employees in addition to the number of subsidiaries each firm has in order to account for the firm size. In addition, we also include the number of patents per employee each firm has obtained in order to correct for the fact that more innovative firms tend to be more productive (see Griffith et al., 2004a; 2004b).[2] We also include information on whether a firm has a foreign subsidiary or not (see below). Finally, εicjt is the residual. Regressions are estimated with standard errors which are two-way clustered by country-sector-year and firm over the years 2006-2015.
The fixed effects in equation (4) also control for various other policy influences and unobserved shocks. For example, previous works show that within industry tariff and input-tariff reductions should also be controlled for (see van der Marel, 2017) as manufacturing sectors are included in our dataset. However, given that tariffs within the EU are set at the Union level (although that’s not the case for the two non-EU countries in our dataset), they are in large part controlled for by the sector-year fixed effects. Moreover, in principle one can construct input tariffs by multiplying tariffs with sector-varying input coefficients. But this variable would nevertheless be dropped from our regressions. This is because tariffs are measured at the EU-level and therefore the analysis would only pick up the variation of the input coefficients and not of any country-sector variation stemming from the restrictiveness. For these reasons, we rely on the fixed effects to control for these policy influences.
Furthermore, another control variable present in previous works is one that measures by year the foreign ownership share of firms. In our case, information on this variable is hard to find because ORBIS does not report such data. However, ORBIS does record whether a firm has a subsidiary in another country or not, which as mentioned above we include as part of the vector of firm-control variables. Taken together, most of our control variables are regrettably omitted in our specification.
4.3 Baseline Extension
In the next step, we expand our baseline specification to take into account any differential impact of data policies regulations on TFP of firms located in a country that is technologically well equipped. The prime reason for doing so is that digital sectors are likely to expand rapidly in countries with the enabling environment ready to transmit and employ electronic data. For instance, countries with qualitatively good telecom networks or with well-penetrated broadband subscriptions are likely to show not only greater levels of activities in data producing sectors, but also in see that downstream sectors reliant on data are affected by data policies in those countries with a better digital enabling environment. This is in line with the recent empirical services literature that has found that domestic institutions matter and can further explain differences in the impact of policies on downstream sectors (see for instance Iootty et al., 2016 and Beverelli et al., 2015).
A well-suited proxy that captures how countries have developed a good digital environment is the WEF’s Network Readiness Indicator (NRI). This indicator measures the capacity of countries to leverage and exploit opportunities offered by ICT for increased competitiveness and well-being (WEF, 2016). This country-specific index summarises various sub-indicators, such as the extent to which individuals are using the internet, international bandwidth in kb/s per user, the country’s availability of latest technologies, as well as the level of technology absorption by firms. All these sub-cases are relevant for our analysis and we therefore include this proxy in our extended regressions.
In the augmented baseline specification, we interact our data linkage ( ) with a demeaned NRI variable varying by country and time. The augmented baseline specification for our cross-country setting therefore is:
 Equation (5) and equation (4) apply a similar set of firm-level control variables with the same set of fixed effects.
Equation (5) and equation (4) apply a similar set of firm-level control variables with the same set of fixed effects.
[1] This is different to Fernandes and Paunov (2012) who use firm-specific services inputs coefficients in the case of services. Although further endogeneity issues may be solved using input-output tables from the first year in our analysis, i.e. 2010, these were unfortunately not available. However, applying input coefficients from a previous year of our time period may also further resolve some potential reverse causality effects in that no endogeneity as a consequence of political economy considerations could exist. This may be the case when sectors with higher TFP levels and which are more dependent on data as inputs lobby for lower restrictions in their country. However, by taking coefficients from the US which is not in our sample and from the year 2007, some of these concerns are avoided. Other endogeneity issues are discussed below in the empirical specification.
[2] Unfortunately, ORBIS does not provide any indication of the amount spent on R&D activities which prevents us from including such variables in our vector of firm-level control variables.
5. Results
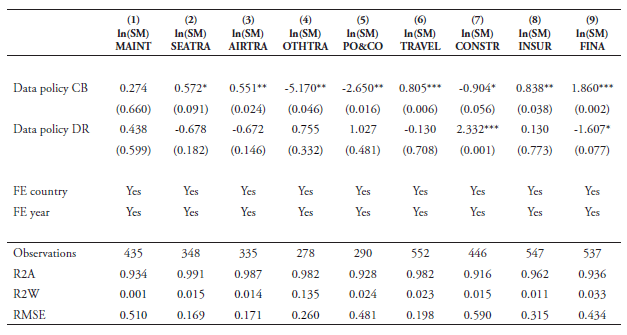
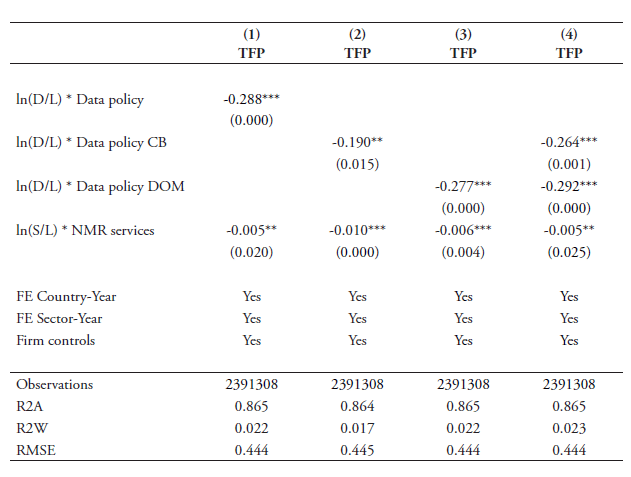
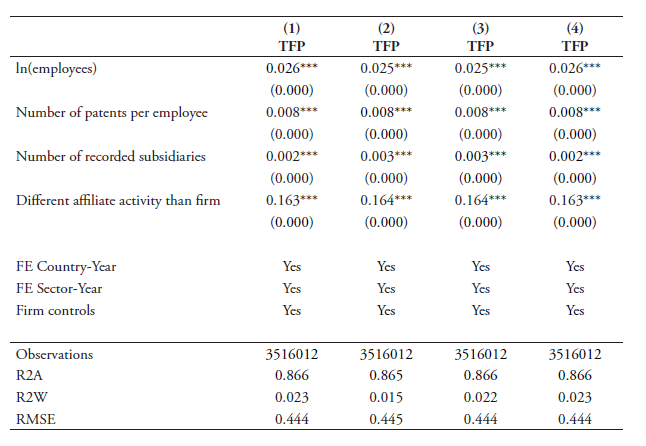
The results of our cross-country baseline estimations are presented in Tables 6 and 7. Column 1 in Table 6 shows that the overall index of data policies is significantly strong with a negative sign. This indicates that countries with a stricter overall framework regarding the use and transfer of data exhibit a significant negative impact on the productivity of firms in those sectors that rely more heavily on data in their production process. Columns 2 and 3 report the coefficient results when breaking up our full index into the two sub-components of cross-border policies and domestic regulatory policies. The results also show that in these two cases, the coefficients are negatively significant at the 1 percent level. Hence, both types of policies have a significant knock-on effect on downstream users of data. Column 4 presents the results when entering the two types of policies together. Both coefficient results are negative and significant.
Table 7 shows the results using alternative TFP measures, which have been outlined in the previous section. The table displays the results for the two different types of data policies when entered together. Column 1 replicates the results using our preferred Ackerberg TFP by means of comparison. Column 2 shows the results for the TFP by Levinsohn and Petrin (2003) and confirms the significance of both sub-indexes of data policies. On the other hand, the TFP specification from Olley and Pakes (1996) shows no significance for the cross-border category of data policies, but nonetheless, the outcome remains strongly significant for the domestic regulatory data policies.
The next two TFP specifications by Hsieh and Klenow (2009; 2014) distinguish between the revenue-based (TFPR) and physical (TFPQ) productivity. These results show that it is only in case of the TFPQ specification that both variables come out as negative and significant. Finally, we have also computed simple labour productivity and used it in the regressions. The results for this proxy show that only domestic regulatory policies come out as significant.
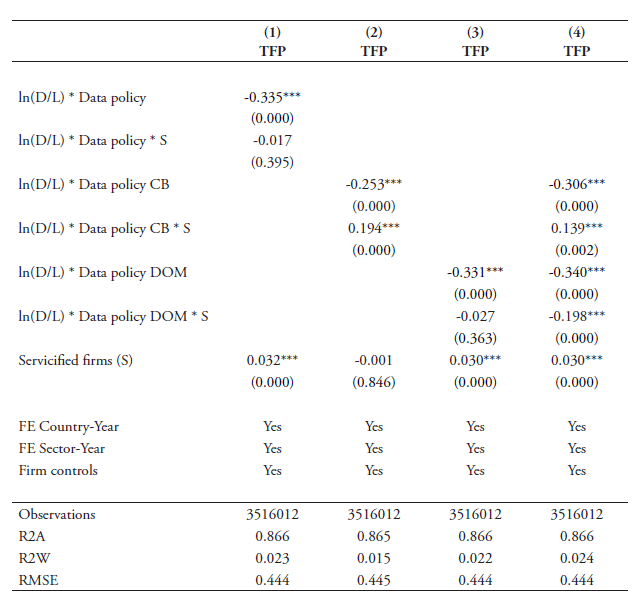
Regarding the extended regressions, Table 8 reports the differential effects of countries having a strong network system that is interacted with our data linkage variable. Again, column 1 of this table shows that the full data policy index has a significant and negative impact at the 1 percent level. In addition, the differential effect is also significant although the coefficient size is relatively small. Yet, it confirms our prior assumption that restrictive data policies have a supplementary adverse effect in countries with a good network environment. In other words, restrictive data regulations in combination with strong network readiness in countries are strong predictors for explaining the performance of TFP of firms in downstream industries that are reliant on data as inputs. This significant result holds for cross-border data policies as illustrated by the relatively high coefficient results in column 2. Yet, no significant effect is found for the interaction term with the data policy index of the domestic use of data in column 3. In addition, Column (4) shows that, when all categories are entered together, the coefficient for the latter interaction term is actually positive. This would mean that firms’ productivity in more digital-enabled countries is less affected by strict data policies on domestic use of data.
An additional extension from our baseline specification is an interaction with a firm-level variable. The ORBIS database shows which manufacturing firms have a services affiliate, as shown in Miroudot and Cadestin (2017). This allows us to assess whether data policies disproportionately hurt so-called servicified firms as opposed to the general effect across all firms in our sample.
To measure this, we create a dummy variable assigning a score of 1 when a manufacturing firm has a service affiliate and zero otherwise. Table 9 shows the results. For the overall data policy index, no significant differential results are found for servicified firms. However, a positive and significant result is found in the interaction term for cross-border data policies. This indicates that cross-border data policies have a less than significant impact on servicified firms. Yet, since the baseline coefficient is significant, but the interaction coefficient size is smaller, it nonetheless suggests that there is significant (negative) differential effect on servicified firms. The results also show that, for domestic policies, no additional effect is found when entered separately. However, when entered together with cross-border policies there is a negative significant result.
5.1 Robustness checks
In this section, we provide several robustness checks for our analysis. In particular, the robustness checks should address concerns on the omission of any regulatory variables in services, on the use of an outdated input-reliance coefficient, and on the fact that the many observations from firm-level data might drive our results. We deal with these concerns below.
5.1.1 Services linkage variable
This robustness check mostly tackles the fact that many services are heavily regulated, and that in turn many services are used also as inputs. This fact may cause concerns that if in the regressions this information is omitted, the results would fail to include a channel of services regulations that may be the prime channel to explain TFP variations in our data. For that reason, we add a services linkage variable that is comprised of a similar interaction term as before: regulatory policies in services sectors are interacted with each downstream sector’s use of services inputs. This follows previous papers on this topic that have established this services linkage variable such as Arnold et al. (2011; 2015). Our services linkage takes the following form:
where φjd and φji come again from the BEA’s input-output tables for the year 2007 reported at the 6-digit level but concorded into the 4-digit NACE. In addition, LABj comes from the BLS also for the year 2007.
The services policy index refers to the country-sector-year specific regulatory indexes in services from the OECD PMR database and consist of the Non-Manufacturing Regulation (NMR) index for six specific sectors, namely: professional services, transportation, utilities, post, retail and telecom services. Their separate interaction results are aggregated into an overall index of services linkages as equation (6) outlines.
The results of including our services linkage control variable are shown in Table 10. First, the services linkage variable comes out very significant in all entries from column (1) – (4). This confirms previous findings in the literature that sectors whose inputs are more services-intense are more affected by regulatory policy changes in services. All data-linkage variables remain robust and significant but have a somewhat lower coefficient size than found in Table 6. The coefficient results on the data linkage variables are much larger than the ones found for the services linkage variables. Yet one should keep in mind that they cannot be directly compared because they are interacted with different policy and intensity values. Also, we have used ln(S/L) as part of the interaction linkage term while previous papers have employed the simple share of services inputs as part of total input use, i.e. (S/IN), and therefore show greater coefficient sizes.
We also regress our baseline equation with the services linkage variable using the share of services inputs in total inputs, (S/IN), as input coefficients in the interaction term. In order to be consistent, we must also use this input share for the data linkage variable. This means that we use the share of data as inputs in total inputs use as well, i.e. (D/IN). Note that in both cases no logs are taken for this share following standard practice in the previous literature. The results are shown in Table 11. In this table, the services linkage variables all come out statistically significant with a negative coefficient sign. All coefficient sizes are much larger than when using the ratio over labour as input coefficients, as expected and in line with previous papers. Regarding the data policy variable, the overall policy index variable and domestic regulatory index variable come out statistically significant as shown in columns (1) and (3) respectively. The cross-border index variable is only weakly significant and falls short of any significance in column (4) when entering the two indexes together.
5.1.2 Alternative data-intensities
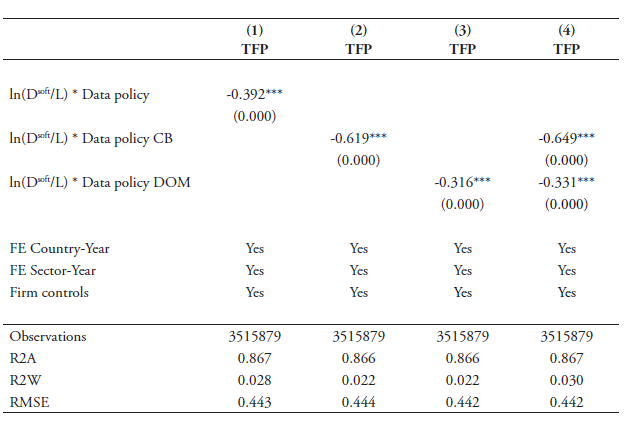
Our second robustness check takes care of the fact that our data-intensity variable may be outdated. Our current data-intensity variables (D/L) and (D/IN) are based on the BEA’s Input Use tables from 2007. Although this gives us an exogenous identification strategy as previously explained, it may run the risk that this data-reliance measure does not capture well the extent to which sectors have undergone extensive increases of data-use over recent years. Therefore, we employ an alternative proxy for data-use from the 2011 US Census Information and Communication Technology (ICT) Survey, which we call Dsoft. These data are survey-based and record at detailed NAICS sector-level how much each industry and service sector spend on ICT in terms of ICT equipment and computer software in million USD.
For our regressions, we take the data on computer software expenditure. The US Census ICT Survey records two separate variables regarding software expenditure, namely non-capitalised and capitalised. We take non-capitalised expenditure in our baseline regression, but similar results appear when using the capitalised software expenditure. Non-capitalised computer software expenditure is comprised of purchases and payroll for developing software and software licensing and service/maintenance agreements for software. Even though this proxy does not entirely capture the extent to which sectors use electronic data, it is nonetheless the nearest alternative variable for data usage we can publicly find. We take the year 2010 for our regressions and divide this software expenditure over labour as we have done in our baseline regression, also for the year 2010. The year 2010 lies somewhere in the middle of our panel analysis. Table B12 in Annex B replicates the Top 10 most and least data-intense sectors with this new intensity proxy.
The results are shown in Table 12. In all cases, our updated data-intensity variables retain their significance as the coefficients are very robust. Interestingly, the coefficient size in column (1) is almost equal to the one reported in column (1) of Table 6. This is also the case for the coefficient result in column (3) for the domestic regulatory restrictions on data. Yet, the coefficient size for the index on cross-border data flows restrictions more than doubles compared to the result in Table 6 and retains its high coefficient size when entered together with the policy index on the domestic use of data in column (4). This outcome may mean that data policies have a particularly high impact on software-intense sectors.
5.1.3 Sector-level Productivity Measures
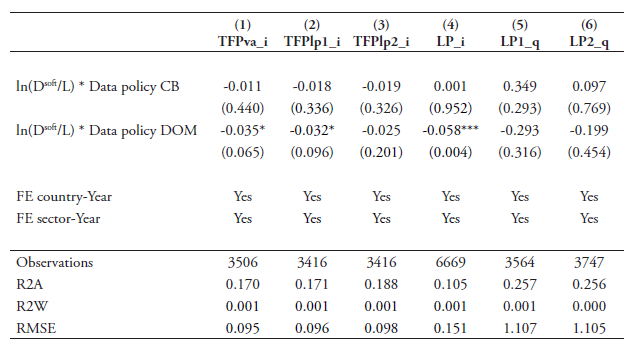
A final potential concern is related to the fact that the high number of observations from firm-level data drives our significant results. Although this should not be of immediate concern as we apply the most stringent clustering effect, it may nonetheless be of interest to use sector-level TFP measures to see whether these results can corroborate our main findings of the baseline regression. There are two ways of using aggregated productivity measures. One is by aggregating our firm-level TFP measures and regressing the baseline specification; the second is using alternative cross-country level TFP measures at the sector-level. Given that the first option may suffer from aggregation problems due to the sample selection, we opt for the second one and we choose a widely accepted database that has established various credible productivity measures in recent years, namely the EU KLEMS.
The EU KLEMS database provides six different TFP and labour productivity (LP) measures that can be used in our regressions, namely (i) TFP value added based growth (TFPva_i); (ii) TFP value added per hour worked based growth (TFPlp1_i); (iii) TFP value added per person employed based growth (TFPlp2_i); (iv) gross value added per hour worked, which is labour productivity (LP_i); (v) growth rate of value added per hour worked (LP1_q); and finally (vi) growth rate of value added per person employed (LP2_q). We use all of them in our regression and replicate the baseline specification presented in Table 7.
Unfortunately, the two non-European countries which we use in the firm-level analysis are left out (i.e. South Korea and Japan), but the US is included as it is available in EU KLEMS. We use a similar time period for our regressions as used with our firm-level data, i.e. 2006-2015. For this specification, we use the updated data-intensity, Dsoft, based on non-capitalised software expenditure over labour first. We also run again the regressions for the capitalised software expenditures over labour.[1]
The results in Table 13 (when using non-capitalised software expenditures over labour) show that the policy restrictions related to cross-border flows of data have a negative coefficient outcome in all cases when using the three different TFP measures but remain insignificant. For the other three labour productivity variables, the coefficient results are positive but also insignificant. The results on restrictions related to domestic regulatory barriers on data show significant negative coefficient outcomes. This is particularly true when using LP_i in column (4) whereas for the two TFP measures in columns (1) and (2) the results are weakly significant. This latter result changes slightly, however, when using capitalised software expenditures over labour as data-intensities as shown in Table 14. In this table, domestic regulatory date policies show somewhat stronger significant results for the two TFP measures in columns (1) and (2).
[1] We also ran regressions using our original data-intensities computed with BEA IO data for the year 2007 with labour from BLS for similar year following equation (2) but without any significant results.
6. Conclusions
For many firms, the increased use of data has become an essential feature of their production processes in the digital era. Firms rely on electronic data and the internet to improve their overall economic performance which we define as productivity in this paper. At the same time, many governments have started to regulate the use and transfer of data over the internet. This paper finds that regulatory policies on data inhibit the productivity performance of firms in data-intense sectors.
The regulatory policies that target data have so far received limited attention in empirical economic studies. In this sense, this paper constitutes a useful contribution by testing whether data regulations have any bearing on the productivity performance of firms. We employ a panel analysis of policy approaches on the cross-border transfer and domestic use of data for a group of developed economies to make a new contribution in the literature on the productivity performance of firms. In particular, we investigate how the productivity of data-intense firms in downstream sectors is affected by stricter data policies. These regulatory policies on data target both the domestic use of data within a country as well as the cross-border flows of data across countries.
The results of our analysis show strong significant evidence that a stricter policy regime on the use and cross-border transfer of data has a negative impact on firms’ economic performance in sectors that rely more on data in their production process. Besides this negative impact, the coefficient size is relatively large meaning the economic impact is substantial. We show that both data policies on the domestic use and cross-border movement of data have a significant effect on productivity. Yet, the results also show that the negative effect is somewhat more robust for the restrictions that apply on the domestic use of use than those policies that restrict the movement of data across borders. This is particularly true when controlling for the additional variables of regulations that may affect productivity, for different proxies for data intensities and when using sector-level productivity data.
Our results suggest that data policies deserve closer attention by policymakers. The economic impact of these measures on local business should be carefully weighed against the policy objective pursued by the government such as privacy or security in order to strike the right balance of what is legitimate regulation without excessively increasing in costs for firms and, eventually, also for consumers. Future research should focus on which measures can better address the concerns of governments related to their non-economic objectives without creating unnecessary costs on firms, that inevitably translate in costs for their own economy. It will be especially important to advance research focussed on developing countries as these countries are imposing today (or planning to impose) the highest level of restrictions on cross-border data flows. While often these measures are driven by industrial policy objectives, this paper shows that strict data policies are more likely to hurt the economy in the long-run than supporting the development of data-intense services in these countries.
References
Ackerberg, D., K. Caves and G. Frazer (2015) “Identification Properties of Recent Production Function Estimators”, Econometrica, Vol. 83, Issue 6, pages 2411-2451.
Arnold, J., B. Javorcik and A. Mattoo (2011) “The Productivity Effects of Services Liberalization: Evidence from the Czech Republic”, Journal of International Economics, Vol. 85, No. 1, pages 136-146.
Arnold, J., B. Javorcik, M. Lipscomb and A. Mattoo (2015) “Services Reform and Manufacturing Performance: Evidence from India”, The Economic Journal, Vol. 126, Issue 590, pages 1-39.
Basu, S., L. Pascali, F. Schiantarelli and L. Serven (2006) “Productivity, Welfare and Reallocation: Theory and Firm-level Evidence”, NBER Working Paper Series No. 15579, Cambridge MA: NBER.
Andrew B. Bernard, A.B., J. Eaton, J. Bradford Jensen and S. Kortum (2003) “Plants and Productivity in International Trade” American Economic Review, Vol. 93, No. 4, pages 1268-1290.
Bauer, M., F. Erixon, H. Lee-Makiyama, M. Krol (2013) “The Economic Importance of Getting Data Protection Right: Protecting Privacy, Transmitting Data, Moving Commerce”, Washington DC: US Chamber of Commerce
Beverelli, C., M. Fiorini and B. Hoekman (2015) “Services Trade Restrictiveness and Manufacturing Productivity: The Role of Institutions”, CEPR Discussion Paper No. 10834, London: CEPR.
Chor, D. (2011) “Unpacking Sources of Comparative Advantage: A Quantitative Approach”, Journal of International Economics, Vol. 82, No 2, pages 152-167.
Christensen, L., A. Colciago, F. Etro and G. Rafert (2013) “The Impact of the Data Protection Regulation in the EU”. Intertic Policy Paper, Intertic.
Duggan, V., S. Rahardja and G. Varela (2013) “Services Reform and Manufacturing Productivity: Evidence from Indonesia”, Policy Research Working Paper Series No. 6349, Washington DC: World Bank.
Ferracane, M.F. (2017), “Restrictions on Cross-Border data flows: a taxonomy”, ECIPE Working Paper No. 1/2018, European Center for International Political Economy, Brussels: ECIPE.
Fernandes, A. and C. Paunov (2012) “Foreign Direct Investment in Services and Manufacturing Productivity: Evidence for Chile”, Journal of Development Economics, Vol. 97, Issue 2, pages 305-321.
Ferracane, M.F., H. Lee-Makiyama and E. van der Marel (2018) “Digital Trade Restrictiveness Index”, European Center for International Political Economy, Brussels: ECIPE.
Gal, P. and A. Hijzen (2016) “The Short-term Impact of Product Market Reforms: A Cross-country Firm-level Analysis”, IMF Working Paper No. WP/16/116, Washington DC: IMF.
Goldfarb, A. and D. Trefler (2018) “AI and International Trade”, NBER Working Paper Series No. 24254, National Bureau of Economic Research, Cambridge MA: NBER.
Goldfarb, A. and C. Tucker (2012) “Privacy and Innovation,” in Innovation Policy and the Economy (eds.) Josh Lerner and Scott Stern, / University of Chicago Press, pages 65–89. See also NBER Working Paper Series No. 17124, National Bureau of Economic Research, Cambridge MA: NBER.
Griffith, R., S. Redding and H. Simpson (2004a) “Foreign Ownership and Productivity: New Evidence from the Service Sector and the R&D Lab”, Oxford Review of Economic Policy, Vol. 20, No. 3, pages 440-456.
Griffith, R., S. Redding and J. van Reenen (2004b) “Mapping the Two Faces of R&D: Productivity Growth in a Panel of OECD Industries”, The Review of Economics and Statistics, Vol. 86, No. 4, pages 883-895.
Hsieh, C-T. and P. Klenow (2009) “Misallocation and Manufacturing TFP in China and India”, Quarterly Journal of Economics, Vol. 124, Issue 4, pages 1403-1448.
Hsieh, C-T. and P. Klenow (2014) “The Life Cycle of Plants in India and Mexico”, Quarterly Journal of Economics, Vol. 129, Issue 3, pages 1035-1084.
Jorgenson, D.W., M.S. Ho and J.D. Samuels (2011) “Information Technology and US Productivity Growth: Evidence from a Prototype Industry Production Account”, Journal of Productivity Analysis, Vol. 2, Issue 36, pages 159-175.
Koske, I., R. Bitetti, I. Wanner and E. Sutherland (2014) “The Internet Economy: Regulatory Challenges and Practices”, OECD Economics Department Working Paper No. 1171, OECD Publishing, Paris.
Levinsohn, J. and A. Petrin (2003) “Estimationg Production Functions Using Input Control for Unobservables”, Review of Economic Studies, Vol. 70, No. 2, pages 317-341.
Melitz, M.J. (2003) “The impact of trade on intra-industry reallocations and aggregate industry productivity”, Econometrica, Vol. 71, pages 1695–725.
Miroudot, S. and C. Cadestin (2017), “Services in Global Value Chains: From Inputs to Value-Creating Activities”, OECD Trade Policy Papers, No. 197, OECD Publishing, Paris.
MIT (2015) “A Business Report on Big Data Gets Personal”, MIT Technology Review, Cambridge MA: MIT.
Nunn, N. (2007) “Relationship-Specificity, Incomplete Contracts, and the Pattern of Trade”, The Quarterly Journal of Economics, Vol. 122(2), pages 569-600.
Olley, S. and A. Pakes (1996) “The Dynamics of Productivity in the Telecommunications Equipment Industry”, Econometrica, Vol. 64, Issue 6, pages 1263-1295.
Siwek, S.E. (2017) “Measuring the US Internet Sector”, Internet Association, Washington DC: IA.
Stone, S., J. Messent and D. Flaig (2015), “Emerging Policy Issues: Localisation Barriers to Trade”, OECD Trade Policy Papers, No. 180, OECD Publishing, Paris.
Opresnik, D. and M. Taisch (2015) “The Value of Big Data in Servicification”, Journal of Production Economics, Vol. 165, pages 174-184.
Iootty, M., J. Kren and E. van der Marel (2016) “Services in the European Union: What Kinds of Regulatory Policies Enhance Productivity?”, World Bank Policy Research Working Paper No. 7919, Washington DC: The World Bank.
van der Marel, E., H. Lee-Makiyama, M. Bauer and B. Verschelde (2016) “A Methodology to Estimate the Costs of Data Regulation”, International Economics, Vol. 146, Issue 2, pages 12-39.
van der Marel, E. (2017) “Explaining Export Dynamics Through Inputs: Evidence from Cross-country Firm-level Data”, Review of Development Economics, Vol. 21, Issue 3, pages 731-755.
World Economic Forum (2015) “Global Information Technology Report 2015: ICTs for Inclusive Growth”, Davos: World Economic Forum.
Tables and Figures
Figure 1: Global data traffic
Source: Cisco (Visual Networking Index); IP stands for Internet Protocol, BP stands for petabyte which is a multiple of the unit byte for digital information, i.e. 10005 bytes
Table 1: Categories covering data policy index and weights
Figure 2: Data policy index over time, all countries (2006-2016)
Source: ECIPE; the line for Data Policies covers both Cross-border (CB) and Domestic (DOM) regulatory policies, which is therefore composed of the two items. All three indexes are a weighted average across the 30 countries in the sample in Table 2 using GDP constant (2010) as weight.
Table 2: Data policy index by country (2017)
Table 3: Data producers
Source: BEA 2007 IO Use Table
Table 4: Top 10 sectors with highest and lowest data use over labour ratio, ln(D/L)
Source: Authors’ calculations using BEA 2007 IO Use Table and BLS.
Table 5: Top 10 sectors with highest and lowest data shares, (D/IN)
Source: Authors’ calculations using BEA 2007 IO Use Table
Figure 3: TFP and data use over labour ratio (D/L) for goods and services, (2013-2015)
Source: Authors’ calculations using BEA 2007 IO Use Table and BLS. This figure omits 2-digit NACE Rev. 2 sector 12 and 47 for being extreme outliers. TFP calculated following Ackerberg et al. (2015) and averaged over 2012-2015. (D/L) is put in logs. In the graph, markers in blue represent manufacturing industries and markers in brown represent services sectors (except accommodation).
Figure 4: TFP and data use over labour ratio (D/L) for services only, (2013-2015)
Source: Authors’ calculations using BEA 2007 IO Use Table and BLS. This figure omits 2-digit NACE Rev. 2 sector 12 and 47 for being extreme outliers. TFP calculated following Ackerberg et al. (2015) and averaged over 2012-2015. (D/L) is put in logs.
Figure 5: TFP and data use share (D/IN) for goods and services, (2013-2015)
Source: Authors’ calculations using BEA 2007 IO Use Table. This figure omits 2-digit NACE Rev. 2 sector 12 for being an extreme outlier. TFP calculated following Ackerberg et al. (2015) and averaged over 2012-2015. (D/IN) is put in logs. In the graph, markers in blue represent manufacturing industries and markers in brown represent services sectors (except accommodation).
Figure 6: Labour productivity and data use over labour (D/L) and share (D/IN), (2013-2015)
Source: Authors’ calculations using BEA 2007 IO Use Table. This figure omits 2-digit NACE Rev. 2 sector 12 for being an extreme outlier. Labour productivity is the logs of value-added over labour and averaged over 2012-2015. (D/IN) and (D/L) are put in logs. In the graph, markers in blue represent manufacturing industries and markers in brown represent services sectors (except accommodation).
Table 6: Baseline regression results
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A.
Table 7: Baseline regression results with alternative TFP measures and labour productivity
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable represents different productivity measures, namely Ackerberg et al. (2015) for ACF; Levinsohn and Petrin (2003) for L&P; Olley and Pakes (1996) for O&P; Hsieh and Klenow (2009; 2014) for TFPR and TFPQ; and value-added per employee for LabPr. All productivity measures are put in logs. Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A.
Table 8: Extended baseline regression results with the NRI interaction term
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A. The variable NRI denotes the Network Readiness Indicator from the WEF and is country-specific and is demeaned.
Table 9: Extended baseline regression results with servicification dummy (S)
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A. The variable S represents a dummy variable when a manufacturing firm has a services affiliate and is firm-specific.
Table 10: Baseline regression results with services linkage control variable
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A. NMR denotes the Non-Manufacturing Regulations policies in services sectors from the OECD’s PMR and is sector-specific but aggregated to country-level.
Table 11: Baseline regression results with services linkage control variable interacted with share
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. (D/IN) denotes the share of data input use in total input use by sector (IN) whereas (S/IN) denotes the share of services input use in total input use by sector. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A. NMR denotes the Non-Manufacturing Regulations policies in services sectors from the OECD’s PMR and is sector-specific, but aggregated to country-level.
Table 12: Baseline regression results with alternative data-intensities
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). Robust standard errors two-way clustered at the country-industry-year and firm level. (Dsoft/L) denotes the ratio of total non-capitalised computer software expenditures over labour by NACE Rev. 2 4-digit sector level, both taken from the US Census for the year 2010. Fixed effects for sector is applied at NACE Rev. 2 4-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A.
Table 13: Baseline regression results with sector-level productivity measures from EU KLEMS (1)
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable represents different productivity measures from EU KLEMs, namely is TFPva_i is TFP value added based growth; TFPlp1_i is TFP value added per hour worked based growth; TFPlp2_i is TFP value added per person employed based growth; LP_i is gross value added per hour worked; LP1_q is growth rate of value added per hour worked; and LP2_q is growth rate of value added per person employed. All productivity measures are put in logs. Robust standard errors clustered at the country-industry-year level. (Dsoft/L) denotes the ratio of total non-capitalised computer software expenditures over labour by NACE Rev. 2 2-digit sector level, both taken from the US Census. Robust standard errors clustered at the country-industry-year level. Fixed effects for sector is applied at NACE Rev. 2 2-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A.
Table 14: Baseline regression results with sector-level productivity measures from EU KLEMS (2)
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable represents different productivity measures from EU KLEMs, namely is TFPva_i is TFP value added based growth; TFPlp1_i is TFP value added per hour worked based growth; TFPlp2_i is TFP value added per person employed based growth; LP_i is gross value added per hour worked; LP1_q is growth rate of value added per hour worked; and LP2_q is growth rate of value added per person employed. All productivity measures are put in logs. Robust standard errors clustered at the country-industry-year level. (Dsoft/L) denotes the ratio of total capitalised computer software expenditures over labour by NACE Rev. 2 2-digit sector level, both taken from the US Census. Robust standard errors clustered at the country-industry-year level. Fixed effects for sector is applied at NACE Rev. 2 2-digit level. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A.
Annex A: Methodology for the data policy index
The data policy index covers those data policies considered to impose a restriction on the cross-border movement and the domestic use of data. The methodology to build the index follows Ferracane et al. (2018b) and covers the measures listed in the Digital Trade Estimates (DTE) database which is available on the ECIPE website (www.ecipe.org/dte/database). Starting from the DTE database, these policies are aggregated into an index using a detailed weighting scheme adapted from Ferracane et al. (2018b). We expand the index released by Ferracane et al. (2018b), which covered only the years 2016/2017, to create a panel for the years 2006-2016 that we can use in our regressions. In addition, the database and index are updated with new regulatory measures found in certain countries.
While certain policies on data flows can be legitimate and necessary to protect the privacy of the individual or to ensure national security, these policies nevertheless create a cost for trade and are therefore included in the analysis. The criteria for listing a certain policy measure in the DTE database are the following: (i) it creates a more restrictive regime for online versus offline users of data; (ii) it implies a different treatment between domestic and foreign users of data; and (iii) it is applied in a manner considered disproportionately burdensome to achieve a certain policy objective.
Each policy measure identified in any of the categories receives a score that varies between 0 (completely open) and 1 (virtually closed) according to how vast its scope is. A higher score represents a higher level of restrictiveness in data policies. The data policy index also varies between 0 (completely open) and 1 (virtually closed). The higher the index, the stricter the data policies implemented in the countries.
The index is composed of two sub-indexes that cover two main types of policy measures that we analyse in this paper: one sub-index covers policies on the cross-border movement of data and one sub-index covers policies on the domestic use of data. Analysing these two sub-indexes separately provides additional information on whether the impact of data policies on services trade varies according to the nature of the policies. The full data policy index is measured as the sum of these two sub-indexes. This annex presents in detail how the two sub-indexes are composed. It shows which policy measures are contained in each of the sub-index and the scheme applied to weigh and score each measure.
The list of measures included in the two sub-indexes is summarised in Table 1. As shown in the table, the sub-indexes are measures as a weighted average of different types of measures. The weights are intended to reflect the level of restrictiveness of the types of measures in terms of costs for digital trade. The first sub-index on cross-border data flows covers three types of measures, namely (i) a ban to transfer data or a local processing requirement for data; (ii) a local storage requirement, and (iii) a conditional flow regime. The second sub-index covers a series of subcategories of policies affecting the domestic use of data. These are: (i) data retention requirements, (ii) subject rights on data privacy, (iii) administrative requirements on data privacy, (iv) sanctions for non-compliance, and finally, (v) other restrictive practices related to data policies.
The main sources used to create the database are national data protection legislations. Otherwise, information is obtained from legal analyses on data policies and regulations from high profile law firms and from OECD (2015). Moreover, occasionally corporate blogs and business reports were also taken into consideration, as they can provide useful information on the de facto regime faced by the company when it comes to movement of data.
1.1 Sub-index on cross-border data flows
The first sub-index covers those policy measures restricting cross-border data flows. These measures are also referred to as “data localisation” measures and can be defined as government imposed measures which result in the localisation of data within a certain jurisdiction. Measures related to data localisation come in various forms and have different degrees of restrictiveness depending on the type of measure itself, but also on the sector and type of data affected.
We identify three types of measures, namely (i) a ban to transfer data or a local processing requirement for data; (ii) a local storage requirement, and (iii) a conditional flow regime. As shown in table 3, the category of bans to transfer and local processing requirements has a score of 0.5, while the other two categories have a score of 0.25 each. The sum of the scores of these categories can go up to 1, that reflects a situation of virtually closed regime on cross-border data flows. This score is multiplied by 0.5 to create the final sub-index on cross-border data flows. The sub-index therefore goes from 0 (completely open) to 0.5 (virtually closed).
Bans to transfer data across the border and local processing requirements are the most restrictive measures on cross-border flow of data. In case of a ban to transfer data or a local processing requirement, the company needs to either build data centres within the implementing jurisdiction or switch to local service providers with a consequent increase in costs if these domestic service providers are less efficient than foreign providers. The difference between bans to transfer and local processing requirements is quite subtle. In the first case, the company is not allowed to even send a copy of the data cross-border. In the second case, the company can still send a copy of the data abroad – which can be important for communication between subsidiary and its parent company and in general for exchange of information within the company. In both cases, however, the main data processing activities need to be done in the implementing jurisdiction.
For the scoring of these measures, both the sectoral coverage of the measure as well as the type of data affected are taken into account. If the ban to transfer or local processing requirement applies to a specific subset of data (for instance, when it applies to health records or accounting data only), this measure receives a scoring of 0.5. A similar score is also assigned when the restriction only applies to specific countries (for instance, when data cannot be sent for processing only to a specific country). On the other hand, when the measure applies to all personal data or data of an entire sector (such as financial services or telecommunication sector), then a score of 1 is given. Measures targeting personal data also receive the highest score because it is often hard to disentangle personal information versus non-personal information, and therefore measures targeting personal data often end up covering the vast majority of data in the economy (MIT, 2015). The score, as always, goes from 0 (completely open) to 1 (virtually closed). Therefore, if there are two measures scoring 0.5, the score is 1. If there are more additional measures, the score for this category still remains one. This score is then weighted by 0.5 which is the weight assigned to the category of bans and local processing requirements (as presented in Table 1).
The second category covers local storage requirements. These measures require a company to keep a copy of certain data within the country. Local storage requirements often apply to specific data such as accounting or bookkeeping data. As long as the copy of the data remains within the national territory, the company can operate as usual. As for the scoring, when data storage is only for specific data as defined above, this measure receives a score of 0.5, whereas when the data storage applies to personal data or to an entire sector, it receives a score of 1. As mentioned before, the score goes up to 1 maximum and is then weighted by 0.25 which is the weight assigned to the category of local storage requirements (as presented in Table 1).
The third category of cost-enhancing measures related to cross-border flow of data is the case of conditional flow regime. These measures forbid the transfer of the data abroad unless certain conditions are fulfilled. If the conditions are stringent, the measure can easily result in a ban to transfer. The conditions can apply either to the recipient country (e.g. some jurisdictions require that data can be transferred only to countries with an “adequate” level of protection) or to the company (e.g. a condition might consist in the need to request the consent of the data subject for the transfer cross-border of his/her data). In terms of scoring, if a conditional flow regime is found, it receives a score of 0.5 in case it applies to specific data, but it receives a score of 1 in case conditions apply for personal data and or the entire sector. The final score is then weighted by 0.25, which is the weight assigned to the category of conditional flow regimes.
Of note, in certain cases it is not easy to discern whether a measure is a ban to transfer, a local processing requirement or a conditional flow regime. In fact, often cases of ban to transfer and local processing requirements have certain exceptions which might de facto result in a conditional flow regime. When the exceptions are quite wide (for example, if they include the request for consent from the data subject), then the measure has been categorized as a conditional flow regime.
Figure A1 shows a graphical representation of the various levels of data localisation measures taken up in this sub-chapter. The direction of the arrow indicates the increased level of restrictiveness. Note that conditional flow regime is put outside this conventional sequence of restrictiveness because it prevents the flow of data only when the conditions are not fulfilled. Also, note that in Table 1 the ban to transfer is put together with local processing requirements although these two measures have actually been separated in Figure A1. The point is that the impact of those measures on trade is very similar and they are not always easy to discern. Yet, a ban to transfer is generally more restrictive than a local processing requirement.
Figure A1: Graphical overview of data policies
Source: Ferracane (2017)
1.2 Sub-index on domestic use of data
The sub-index on domestic use of data index covers a series of subcategories of policies affecting the domestic use of data. These are: (i) data retention requirements, (ii) subject rights on data privacy, (iii) administrative requirements on data privacy, (iv) sanctions for non-compliance, and finally, (v) other restrictive practices related to data policies. Given that each of these sub-categories contains, in turn, additional sub-categories, they will be presented separately. For the calculation of the sub-index, the weights assigned to the categories are shown in Table 3. The categories with the highest weights (and therefore those which are considered to create higher costs for digital trade) are data retention and administrative requirements on data privacy, which are assigned a weight of 0.15 each. The category of subject rights on data privacy is assigned a score of 0.1, while the other two categories of sanctions for non-compliance and other restrictive practices are assigned a score of 0.05.
The sum of the scores of these categories can go up to 0.5 that reflect a situation of virtually closed regime on domestic use of data. The sub-index therefore goes from 0 (completely open) to 0.5 (virtually closed). As mentioned above, the data policy index is measured as the sum of the two sub-indexes and therefore the score for the final data policy index goes from 0 to 1.
1.2.1 Data retention
The first category belonging to the sub-index on domestic use of data deals with measures related to data retention, which are measures regulating how and for how long a company should keep certain data within its premises. Data retention measures can define a minimum period of retention or a maximum period of retention. In the first case, the companies (often telecommunication companies) are required to retain a set of data of their users for a certain period, which can go up to two years or more in some cases. These measures can be quite costly for the companies and they are assigned a weight of 0.7. On the other hand, the measures imposing a maximum period of retention are somewhat less restrictive and prescribe the company not to retain certain data when it is not needed anymore for providing their services. They are therefore given a weight of 0.3. The country receives a score of 1 in each of the two sub-categories when there is a one or more measures implemented, while 0 is assigned in case of absence of these measures. Therefore, if a country implements one or more data retention requirements for a minimum period of time and no data retention requirements for a maximum period of time, the score will be 0.7. Alternatively, if the country only implements one requirement of maximum period of data retention, the score will be 0.3.
1.2.2 Subject rights on data privacy
The second category belonging to the sub-index on domestic use of data includes measures related to subject rights on data privacy. The rights of the data subject are often a legitimate goal in itself, but they can nonetheless represent a cost for the firm when they are implemented disproportionately or in a discriminatory manner. This is the reason why they are covered in the database. However, they only form a smaller part of the sub-index with a weight of 0.1 as their cost on business is significantly low compared with other measures. Two categories of measures are identified regarding data subject rights, which are (i) the need for consent for the collection and use of data (with a weight of 0.5) and (ii) the right to be forgotten (with also a weight of 0.5).
If one of the measures applies, a score of 1 is given whereas a score of 0 is assigned otherwise. Regarding the first measure on the request of consent for the collection and use of data, a score of 1 is given only when the process for requesting consent is considered as disproportionately burdensome. This is the case when the consent has to be always written and explicit or when consent is required not only for the collection of data, but also for any transfer of data outside the collecting company. If this is not the case, then a score of 0 is assigned. Additionally, important to note is that, if the consent is required only in case of transfer across borders, this measure is instead reported in the first sub-index under conditional flow regime and scored accordingly.
1.2.3 Administrative requirements on data privacy
The third category belonging to the sub-index on domestic use of data covers administrative requirements on data privacy. Measures included in this category are (i) the requirement to perform a data privacy impact assessment (DPIA) (with a weight of 0.3), (ii) the requirement to appoint a data protection officer (DPO) (with as well a weight of 0.3), (iii), the requirement to notify the data protection authority in case of a data breach (with a weight of 0.1), and finally (iv) the requirement to allow the government to access the personal data that is collected (with also a weight of 0.3).
For the scoring, the first two measures receive a score of 1 when a measure applies and 0 otherwise. In the case of the fourth measure, which is the requirement to allow government to access collected personal data, a full score of 1 is assigned only when the government has an open access to data in at least one sector of the economy. However, if a government has only access to escrow or encryption keys, but still notifies access to the data, an intermediate score of 0.7 is assigned. Government direct access to data handled by the company or the use of escrow keys may in fact create remarkable consumer dissatisfaction that may lead to the user’s termination of service demand. Finally, if the government has to follow the same procedure that it would follow for offline access to data – that is, the presence of a court decision or a warrant, or when the request follows a judicial investigation process – then the score is 0.
1.2.4 Sanctions for non-compliance
The fourth category belonging to the sub-index on domestic use of data examines measures which impose a sanction for non-compliance. These measures cover both pecuniary and penal sanctions with a weight of 0.5 for each of them. The pecuniary sanctions are not considered a restriction per se, but their presence is listed in the database and accounted for in the sub-index when (i) they are above 250,000 EUR; (ii) companies have explicitly complained about disproportionately high fines or discriminatory enforcement of sanctions; (iii) they are expressed as a percentage of a company’s domestic or global turnover. In fact, in all these cases, the sanctions have the capacity of putting a company out of business and might play an important role in the economic calculation of a company. We also list under this section those instances in which the infringement of data privacy rules can be sanctioned by closing down the business. On the other hand, the application of penal sanctions such as jail-time as a result of infringement of data privacy rules is included in the database as a restriction. Instances in which penal sanctions are assigned as a result of identity theft and similar illegal actions are obviously not included. For what concerns the scoring, if these cases are identified, a score of 1 is assigned.
1.2.5 Other measures
Finally, the last category takes up all those measures which are related to domestic use of data, but do not fit under any of the aforementioned categories. All these measures are assigned a score of 1.
Annex B: Additional Tables and Figures
Table B1: Number of firms by year
Source: ORBIS. Note: sample contains only firms that have at least 4 years of data.
Table B2: Sector division with frequency numbers of firms from ORBIS in TFP dataset
Source: ORBIS. Note: for the production functions estimates, some countries are grouped together due to unreported or insufficient data, as explained in the main text. Malta and Cyprus are not included in TFP estimates.
Table B3: Sector division with frequency numbers of firms from ORBIS in TFP dataset (continued), services
Source: ORBIS. Note: for the production functions estimates, some countries are grouped together due to unreported or insufficient data, as explained in the main text. Malta and Cyprus are not included in TFP estimates.
Table B4: Number of firms by country
Source: ORBIS. Notes: Malta and Cyprus are not included in TFP estimates.
Table B5: Correlation regressions between directly reported and indirectly computed material inputs for countries included firms
Note: * p<0.10; ** p<0.05; *** p<0.01.
Table B6: List of countries
Table B7: Summary statistics of variables used in production function
Note: Y denotes the value-added, K denotes capital and is computed using the Perpetual Inventory Method (PIM)., L denotes the number of employees, M denotes materials and Inv denotes investments. All variables have used sectoral deflators.
Table B8: Summary statistics of TFP estimates and labour productivity
Note: The TFP measures from Ackerberg et al. (2015) is for ACF; Levinsohn and Petrin (2003) for L&P; Olley and Pakes (1996) for O&P; Hsieh and Klenow (2009; 2014) for TFPR and TFPQ; and value-added per employee used for LabPr. All productivity measures are put in logs.
Table B9: Pairwise correlation table between the TFP measures
Note: The TFP measures from Ackerberg et al. (2015) is for ACF; Levinsohn and Petrin (2003) for L&P; Olley and Pakes (1996) for O&P; Hsieh and Klenow (2009; 2014) for TFPR and TFPQ; and value-added per employee used for LabPr. All productivity measures are put in logs.
Table B10: Summary country, sector and firm-level variables
Note: The sector-level variables of intensities, i.e. ln(D/L), ln(S/L), (D/IN) and (S/IN) are sourced from the BEA 2007 IO Use Table and BLS, but concorded into NACE Rev. 2 4-digit level. Therefore, summary statistics are shown at NACE Rev. 2 4-digit level. NMR denotes the Non-Manufacturing Regulations policies in services sectors from the OECD’s PMR and is sector-specific but aggregated to country-level in the regressions. CB denotes Cross-Border and covers all policies outlined under 1.1 in Annex A. DOM denotes Domestic and covers all policies outlined under 1.2-1.6 in Annex A. The variable NRI denotes the Network Readiness Indicator from the WEF and is used in its demeaned version in the regressions.
Figure B1: Kernel density estimate Data Policy variable
Source: Ferracane et al. (2018). The Kernel density estimate is done for the overall Data Policy variables as taken up in all regressions with N=65*6 for all countries and years covered in the DTRI.
Figure B2: Kernel density estimate ln(D/L) * Data Policy
Source: Ferracane et al. (2018) for Data policy. The Kernel density estimate is done for the overall Data Policy variables as taken up in all regressions with N=26*6*478 for all countries, years and sectors covered in the regressions.
Table B11: Firm-level control variables
Note: * p<0.10; ** p<0.05; *** p<0.01. The dependent variable is in logs and follows Ackerberg et al. (2015). The columns of this table follow the order of the baseline regression specifications as presented in Table 6. Robust standard errors two-way clustered at the country-industry-year and firm level. Fixed effects for sector is applied at NACE Rev. 2 4-digit level.
Table B12: Top 10 sectors with highest and lowest data use over labour ratio, ln(D/L), using the US Census ICT Survey for the year 2010
Source: Authors’ calculations using US Census ICT Survey and BLS.